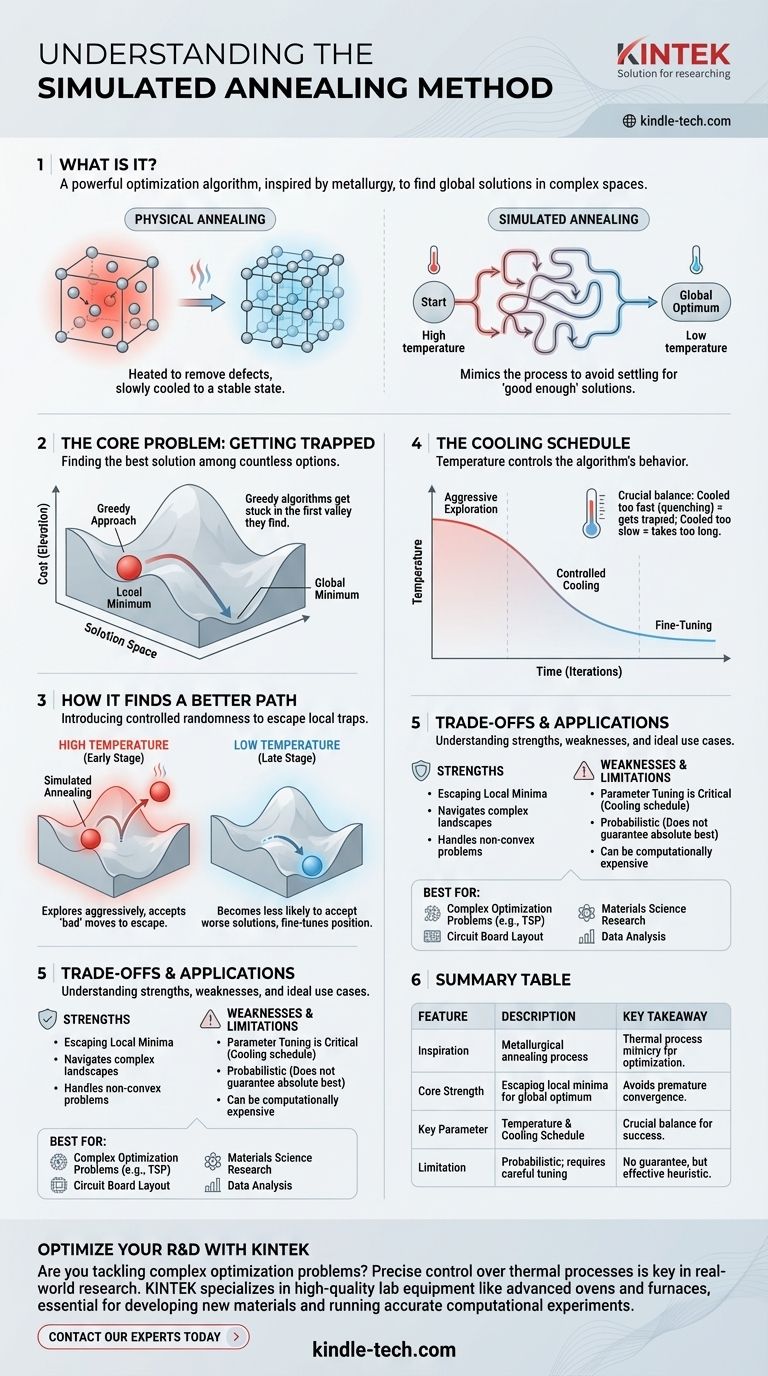
En bref, le recuit simulé est un puissant algorithme d'optimisation utilisé pour trouver une bonne (et souvent globale) solution dans un espace de recherche vaste et complexe. Il est directement inspiré du processus métallurgique de recuit, où un matériau est chauffé puis lentement refroidi pour éliminer les défauts et atteindre un état cristallin stable et de basse énergie. L'algorithme imite ce processus physique pour résoudre des problèmes computationnels abstraits.
À la base, le recuit simulé évite le piège courant de se contenter d'une solution "suffisamment bonne" en imitant le processus physique de recuit du métal. Il commence par explorer un large éventail de possibilités (haute température) et réduit progressivement son champ d'action pour trouver une solution stable et de haute qualité (basse température).
Le problème central : rester piégé
Pour comprendre le recuit simulé, vous devez d'abord comprendre le problème qu'il résout : trouver la meilleure solution possible parmi d'innombrables options, une tâche connue sous le nom d'optimisation.
Le paysage des solutions
Imaginez que chaque solution possible à votre problème est un point sur un vaste paysage vallonné. L'élévation de chaque point représente son "coût" — plus l'élévation est basse, meilleure est la solution. Votre objectif est de trouver le point le plus bas de toute la carte, le minimum global.
L'approche "gourmande" et son défaut
Un algorithme simple, souvent appelé "escalade de colline" (hill-climbing), commencerait à un point aléatoire et descendrait toujours. C'est une approche "gourmande" car elle n'accepte que les mouvements qui apportent une amélioration immédiate.
Le problème est que cette méthode se retrouvera bloquée dans la première vallée qu'elle trouve — un minimum local. Elle n'a aucun moyen de savoir si une vallée beaucoup plus profonde, le minimum global, existe juste derrière la prochaine colline.
Comment le recuit simulé trouve un meilleur chemin
Le recuit simulé surmonte cette limitation en introduisant un élément de hasard contrôlé qui lui permet d'échapper à ces pièges locaux.
L'inspiration : le recuit physique
En métallurgie, le chauffage d'un métal donne à ses atomes suffisamment d'énergie pour se déplacer librement, brisant les structures sous-optimales et défectueuses. Lorsque le métal est refroidi lentement, les atomes ont le temps de s'installer dans un réseau cristallin très ordonné et solide — un état d'énergie minimale.
L'algorithme : la température comme bouton de contrôle
Le recuit simulé adopte ce concept en introduisant un paramètre de température. Ce n'est pas une température physique, mais une variable qui contrôle le comportement de l'algorithme.
L'algorithme commence avec une température élevée. Dans cet état, il explore agressivement le paysage des solutions, un peu comme les atomes énergétiques dans le métal chaud. Il a une forte probabilité d'accepter des mouvements qui sont pires que sa position actuelle. C'est la clé : faire un "mauvais" mouvement est ce qui lui permet de sortir d'un minimum local.
Le programme de refroidissement
Au fur et à mesure que l'algorithme s'exécute, la température est progressivement abaissée selon un programme de refroidissement. À mesure que la température diminue, l'algorithme devient de moins en moins susceptible d'accepter une solution moins bonne.
À la fin, à très basse température, l'algorithme se comporte comme la simple méthode d'escalade de colline, n'acceptant que les améliorations et affinant sa position dans ce qui est, espérons-le, le minimum global.
Comprendre les compromis
Comme tout outil puissant, le recuit simulé n'est pas une solution universelle. Comprendre ses limites est essentiel pour l'utiliser efficacement.
Force : Échapper aux minima locaux
Son principal avantage est sa capacité à naviguer dans des paysages complexes et non convexes avec de nombreux minima locaux. Pour les problèmes où les algorithmes gourmands échouent systématiquement, le recuit simulé est un excellent choix.
Faiblesse : Le réglage des paramètres est crucial
La performance de l'algorithme est très sensible au programme de refroidissement. S'il est refroidi trop rapidement, il peut quand même se retrouver piégé dans un minimum local ("trempe"). S'il est refroidi trop lentement, il peut prendre un temps irréalisable pour trouver une solution. Trouver le bon programme nécessite souvent des expérimentations.
Limitation : C'est une méthode probabiliste
Le recuit simulé ne garantit pas qu'il trouvera la meilleure solution absolue (le minimum global). C'est une heuristique, ce qui signifie qu'il est conçu pour trouver une très bonne solution en un temps raisonnable. Il y a toujours une chance statistique qu'il se fixe dans un état sous-optimal.
Faire le bon choix pour votre problème
Utilisez ces conseils pour décider si le recuit simulé est l'approche correcte pour votre tâche d'optimisation.
- Si votre objectif principal est de résoudre un problème complexe avec de nombreux pièges (minima locaux) : Le recuit simulé est l'un des meilleurs outils pour cette tâche, en particulier pour des problèmes classiques comme le problème du voyageur de commerce ou la conception de circuits imprimés.
- Si votre objectif principal est de trouver une solution prouvablement optimale avec une vitesse maximale : Vous devriez d'abord vérifier si votre problème est suffisamment simple (par exemple, convexe) pour être résolu par un algorithme plus rapide et déterministe comme la programmation linéaire ou une approche gourmande standard.
En fin de compte, le recuit simulé fournit un cadre robuste pour naviguer dans des espaces de recherche vastes et difficiles afin de trouver des solutions de haute qualité là où les méthodes plus simples échouent.
Tableau récapitulatif :
| Caractéristique | Description |
|---|---|
| Inspiration | Processus de recuit métallurgique (chauffage & refroidissement lent) |
| Force principale | Échapper aux minima locaux pour trouver un optimum global |
| Paramètre clé | Température & Programme de refroidissement |
| Idéal pour | Problèmes d'optimisation complexes avec de nombreux pièges locaux |
| Limitation | Probabiliste ; nécessite un réglage minutieux des paramètres |
Optimisez votre recherche et développement avec KINTEK
Vous abordez des problèmes d'optimisation complexes en science des matériaux, en génie chimique ou en analyse de données ? Les principes du recuit simulé sont inspirés de processus thermiques réels, et un contrôle précis de ces processus dans votre laboratoire est crucial.
KINTEK est spécialisé dans les équipements de laboratoire de haute qualité, y compris les fours et étuves avancés qui offrent le chauffage uniforme et le refroidissement contrôlé essentiels à la recherche et au développement. Que vous développiez de nouveaux matériaux ou que vous meniez des expériences computationnelles, un équipement fiable est la base de résultats précis.
Contactez nos experts dès aujourd'hui pour trouver la solution de laboratoire parfaite afin d'améliorer vos flux de travail d'optimisation et d'obtenir des résultats révolutionnaires.
Produits associés
- Four à atmosphère hydrogène
- Petit four de frittage de fil de tungstène sous vide
- Four à atmosphère contrôlée à bande maillée
- 1400℃ Four à atmosphère contrôlée
- Matrice d'étirage revêtement nano-diamant HFCVD Equipment
Les gens demandent aussi
- À quoi servent les fours à hydrogène ? Atteignez pureté et rapidité dans le traitement à haute température
- À quoi sert un four à atmosphère ? Obtenez un traitement thermique précis et sans contamination
- Pourquoi l'hydrogène est-il utilisé dans les fours de frittage ? La clé d'une pureté et d'une résistance supérieures
- Quelles précautions de sécurité devez-vous prendre lorsque vous travaillez avec une source de chaleur ? Directives essentielles pour un environnement de laboratoire sûr
- Quelle est la différence entre l'atmosphère modifiée et l'atmosphère contrôlée ? Maîtriser les méthodes de conservation des aliments
