Comment la taille de l'échantillon affecte-t-elle l'analyse ? Maximisez la fiabilité de votre recherche

En bref, la taille de l'échantillon est le facteur le plus important déterminant la fiabilité et la précision de vos résultats analytiques. Une taille d'échantillon plus grande et correctement sélectionnée augmente votre confiance que les résultats ne sont pas dus au hasard, offrant une représentation plus précise de l'état réel de la population sous-jacente que vous étudiez.

Le point essentiel à retenir est que la taille de l'échantillon ne consiste pas seulement à collecter plus de données ; c'est une décision stratégique qui contrôle directement deux facteurs critiques : votre capacité à détecter un effet réel (puissance statistique) et la certitude de vos mesures (précision).

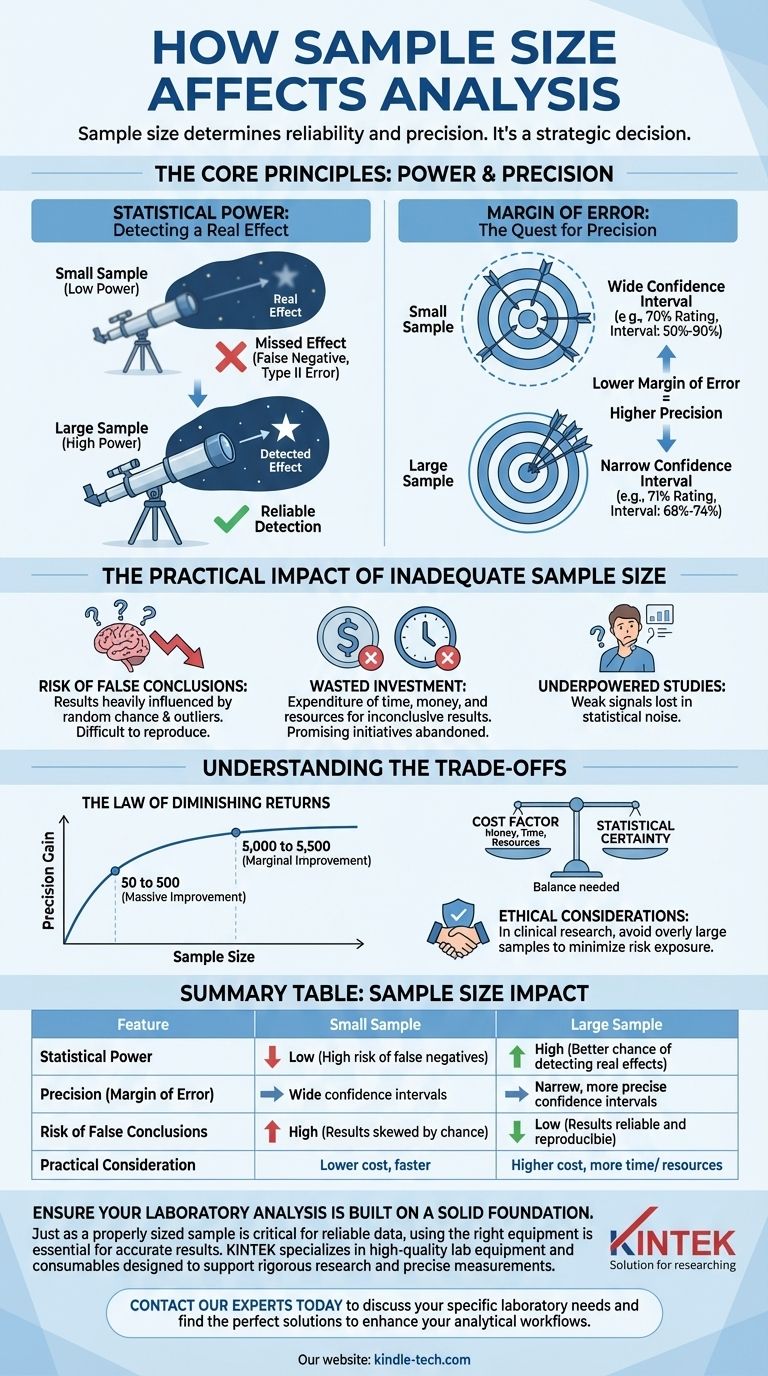
Les principes fondamentaux : Puissance et Précision

Pour comprendre l'impact de la taille de l'échantillon, vous devez saisir les deux concepts fondamentaux qu'elle régit. Ces principes expliquent pourquoi "plus c'est souvent mieux" dans l'analyse des données.

Puissance statistique : La capacité à détecter un effet

La puissance statistique est la probabilité que votre étude détecte un effet qui existe réellement. C'est comme avoir un télescope suffisamment puissant pour voir une étoile lointaine.

Une petite taille d'échantillon est un télescope de faible puissance. Même si un effet réel et important est présent (le bénéfice d'un médicament révolutionnaire, une campagne marketing réussie), une étude sous-alimentée est susceptible de le manquer entièrement.

Cela conduit à une erreur de type II, ou un faux négatif. Vous concluez à tort qu'il n'y a pas d'effet alors qu'en fait, il y en a un.

Marge d'erreur : La quête de précision

La marge d'erreur décrit la précision de vos résultats. Elle crée un intervalle de confiance, qui est une fourchette dans laquelle vous pouvez être raisonnablement sûr que se trouve la vraie valeur pour l'ensemble de la population.

Avec un petit échantillon, votre marge d'erreur est grande. Vous pourriez constater qu'un nouveau produit a un taux de satisfaction de 70 %, mais votre intervalle de confiance est de 50 % à 90 %. Cette fourchette est trop large pour être utile à la prise d'une décision commerciale.

À mesure que la taille de votre échantillon augmente, la marge d'erreur diminue. Un échantillon plus grand pourrait vous donner une note de 71 % avec un intervalle de confiance beaucoup plus étroit de 68 % à 74 %. Il s'agit d'une information précise et exploitable.

L'impact pratique d'une taille d'échantillon inadéquate

Choisir une taille d'échantillon trop petite est l'une des erreurs analytiques les plus courantes. Elle compromet votre travail et peut entraîner des erreurs de jugement coûteuses.

Risque de fausses conclusions

Le principal danger d'un petit échantillon est que vos résultats sont fortement influencés par le hasard et les valeurs aberrantes. Vous pourriez observer un schéma fort qui disparaît complètement lorsque davantage de données sont collectées.

Cela rend vos résultats difficiles à reproduire, ce qui est une pierre angulaire de la recherche et de l'analyse crédibles.

Investissement gaspillé dans la recherche

Une étude sous-alimentée est souvent un investissement gaspillé. Vous dépensez du temps, de l'argent et des ressources pour n'arriver qu'à un résultat peu concluant.

Pire encore, un faux négatif pourrait vous amener à abandonner une initiative, un produit ou une ligne de recherche prometteurs parce que le signal faible a été perdu dans le bruit statistique.

Comprendre les compromis

Bien qu'une taille d'échantillon plus grande soit statistiquement supérieure, des contraintes pratiques jouent toujours un rôle. L'objectif n'est pas de collecter la quantité maximale de données possible, mais la quantité optimale.

La loi des rendements décroissants

Le bénéfice statistique que vous obtenez en augmentant la taille de votre échantillon n'est pas linéaire. L'amélioration de 50 à 500 participants est massive. L'amélioration de 5 000 à 5 500 est marginale.

À un certain point, le coût de la collecte de données supplémentaires l'emporte sur le faible gain de précision que vous obtiendrez.

Le facteur coût : Temps et ressources

La collecte de données est souvent la partie la plus coûteuse et la plus longue d'un projet. Chaque point de données a un coût en termes d'argent, de main-d'œuvre et de puissance de calcul.

Vous devez équilibrer le besoin de certitude statistique avec le budget et le calendrier de votre projet.

Considérations éthiques

Dans des domaines comme la recherche clinique, l'utilisation d'un échantillon trop grand peut être contraire à l'éthique. Cela peut exposer plus de participants que nécessaire à des risques potentiels ou refuser à un groupe de contrôle l'accès à un traitement supérieur plus longtemps que nécessaire.

Faire le bon choix pour votre objectif

La taille optimale de votre échantillon dépend entièrement de l'objectif de votre analyse. Une "analyse de puissance" formelle est la méthode standard pour la calculer, mais une compréhension conceptuelle guidera votre stratégie.

• Si votre objectif principal est la recherche exploratoire précoce : Un échantillon plus petit et plus flexible peut être acceptable pour identifier des signaux potentiels ou tester une hypothèse de manière directionnelle, en comprenant parfaitement que les résultats ne sont pas définitifs.
• Si votre objectif principal est la prise de décision à enjeux élevés (par exemple, un essai clinique ou un investissement de plusieurs millions de dollars) : Un échantillon plus grand et statistiquement significatif est non négociable. Le coût de l'erreur est bien trop élevé pour risquer une étude sous-alimentée.
• Si votre objectif principal est de comprendre une population (par exemple, un sondage politique national) : Votre priorité est une faible marge d'erreur. Une taille d'échantillon suffisante est requise pour garantir que la précision de vos estimations reflète fidèlement la population réelle.

Dimensionner correctement votre échantillon n'est pas seulement une formalité statistique ; c'est le fondement sur lequel chaque conclusion crédible est construite.

Tableau récapitulatif :

Impact de la taille de l'échantillon	Petit échantillon	Grand échantillon
Puissance statistique	Faible (risque élevé de faux négatifs)	Élevée (meilleure chance de détecter des effets réels)
Précision (Marge d'erreur)	Intervalles de confiance larges	Intervalles de confiance étroits et plus précis
Risque de fausses conclusions	Élevé (résultats facilement faussés par le hasard)	Faible (les résultats sont plus fiables et reproductibles)
Considération pratique	Coût inférieur, plus rapide	Coût supérieur, plus de temps/ressources

Assurez-vous que votre analyse de laboratoire repose sur des bases solides.

Tout comme une taille d'échantillon correctement dimensionnée est essentielle pour des données fiables, l'utilisation du bon équipement est cruciale pour des résultats précis. KINTEK est spécialisé dans les équipements de laboratoire et les consommables de haute qualité conçus pour soutenir une recherche rigoureuse et des mesures précises.

Laissez-nous vous aider à avoir confiance en vos données. Contactez nos experts dès aujourd'hui pour discuter de vos besoins spécifiques en laboratoire et trouver les solutions parfaites pour améliorer vos flux de travail analytiques.