Comment la taille de l'échantillon affecte-t-elle la précision nécessaire de la mesure ? Optimisez la qualité de vos données

En bref, une plus grande taille d'échantillon ne modifie pas la précision inhérente de votre instrument de mesure, mais elle augmente considérablement la précision des conclusions que vous pouvez tirer de vos données. En collectant plus d'échantillons, vous réduisez l'« erreur d'échantillonnage », qui est l'incertitude résultant de l'observation d'une partie d'un groupe au lieu de l'ensemble. Cela signifie que vos résultats sont plus susceptibles d'être une représentation fidèle de l'ensemble de la population.

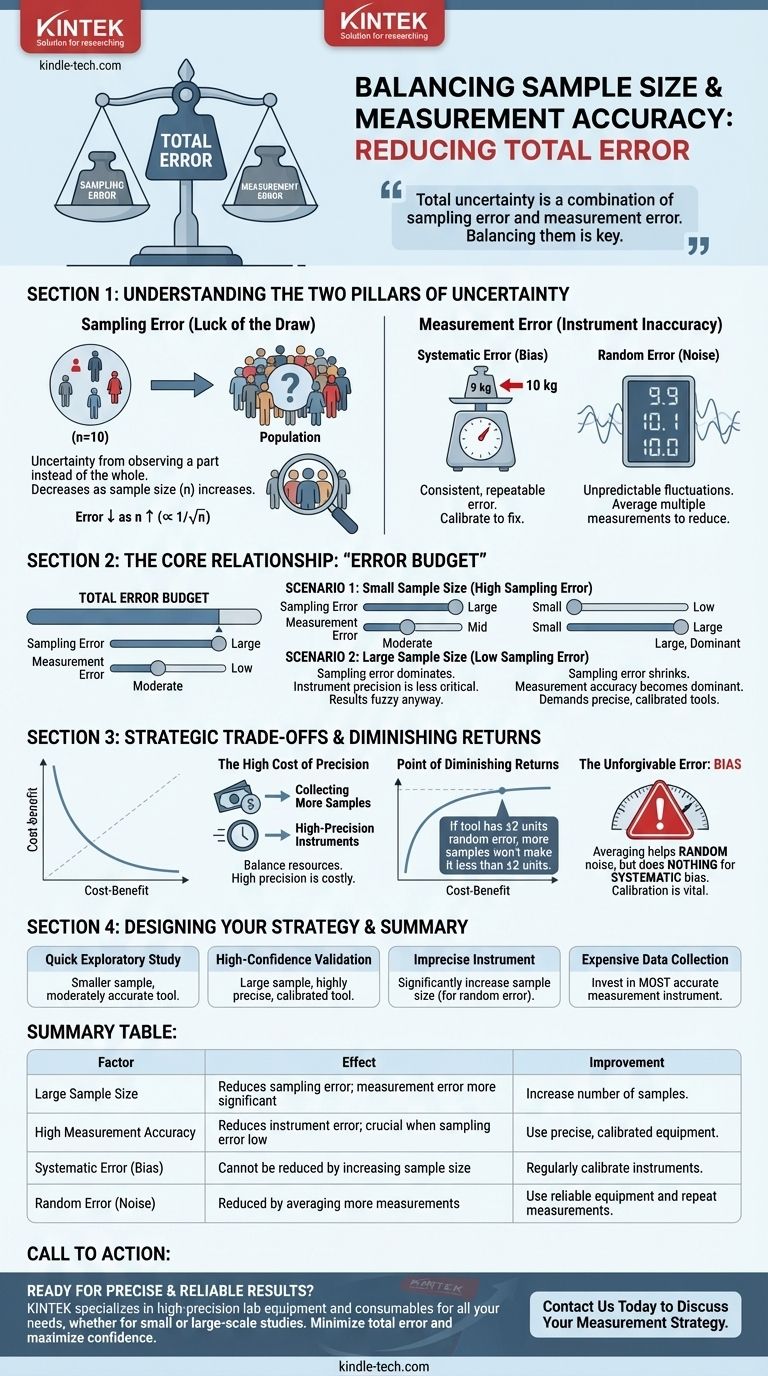
Le problème fondamental ne concerne pas seulement la taille de l'échantillon ; il s'agit d'équilibrer deux sources d'erreur distinctes. Votre incertitude totale est une combinaison de l'erreur d'échantillonnage (due à la taille de votre échantillon) et de l'erreur de mesure (due à la qualité de votre outil). Comprendre comment ces deux interagissent est la clé pour concevoir une étude efficace.

Les deux piliers de l'incertitude : Échantillonnage vs Mesure

Pour saisir pleinement la relation, vous devez distinguer les deux types fondamentaux d'erreur qui peuvent affecter vos résultats. Ils ne sont pas interchangeables.

Comprendre l'erreur d'échantillonnage

L'erreur d'échantillonnage est le « coup de chance ». C'est la différence aléatoire entre les caractéristiques de votre échantillon et les caractéristiques de l'ensemble de la population qu'il est censé représenter.

Imaginez que vous essayiez de déterminer la taille moyenne de toutes les personnes d'une ville en mesurant seulement 10 individus. Vous pourriez accidentellement choisir un groupe exceptionnellement grand ou petit.

Cette erreur n'est pas une faute ; c'est une réalité statistique. La bonne nouvelle est qu'elle est prévisible et peut être contrôlée. À mesure que la taille de votre échantillon (n) augmente, votre erreur d'échantillonnage diminue à un taux proportionnel à la racine carrée de la taille de l'échantillon (1/√n). Un échantillon plus grand est plus susceptible de refléter la vraie population.

Comprendre l'erreur de mesure

L'erreur de mesure est l'imprécision inhérente à votre appareil ou méthode de mesure. Elle n'a rien à voir avec le nombre d'échantillons que vous prélevez.

Cette erreur se présente sous deux formes :

1. Erreur systématique (biais) : Une erreur cohérente et reproductible. Pensez à une balance qui indique toujours 1 kg de trop. Prendre plus de mesures ne corrigera pas cela ; vous obtiendrez simplement une réponse très précise, mais fausse.
2. Erreur aléatoire (bruit) : Fluctuations imprévisibles dans la mesure. Pensez à une balance numérique dont le dernier chiffre clignote légèrement.

Faire la moyenne de nombreuses mesures peut aider à réduire l'effet de l'erreur aléatoire, mais cela ne peut jamais corriger l'erreur systématique. La précision de votre outil crée une limite stricte à la véracité ultime de vos données.

Comment la taille de l'échantillon et la précision des mesures interagissent

L'idée cruciale est que ces deux erreurs contribuent à votre « budget d'erreur » total. Votre objectif est de minimiser l'erreur totale, et la manière dont vous allouez les ressources pour combattre chaque type d'erreur dépend de votre situation.

La relation fondamentale : Votre « budget d'erreur »

Considérez votre niveau de confiance souhaité comme un budget pour l'erreur totale. Vous « dépensez » ce budget en une combinaison d'erreur d'échantillonnage et d'erreur de mesure.

Si une source d'erreur est très importante, elle dominera vos résultats, et la réduction de l'autre source peut avoir peu d'effet pratique.

Scénario 1 : Petite taille d'échantillon

Lorsque la taille de votre échantillon est petite, l'erreur d'échantillonnage est élevée. C'est presque toujours le plus grand contributeur à votre incertitude totale.

Dans cette situation, la précision de votre outil de mesure est moins critique. Votre résultat sera de toute façon flou en raison du « coup de chance » de l'échantillonnage, donc une petite quantité d'erreur de mesure n'aggravera pas beaucoup l'image globale.

Scénario 2 : Grande taille d'échantillon

À mesure que vous augmentez la taille de votre échantillon, l'erreur d'échantillonnage diminue considérablement. La moyenne de votre échantillon se rapproche de plus en plus de la vraie moyenne de la population.

C'est là que la question de l'utilisateur devient particulièrement pertinente. Une grande taille d'échantillon augmente efficacement l'exigence de précision de la mesure. À mesure que l'erreur d'échantillonnage disparaît, toute erreur provenant de votre instrument devient la source dominante d'incertitude.

Si votre outil de mesure présente un biais systématique, une taille d'échantillon énorme ne fera que vous donner une estimation très précise d'une valeur erronée. Cela amplifie l'importance d'avoir un instrument bien calibré et précis.

Comprendre les compromis

Décider de la taille de l'échantillon et de la qualité de l'instrument est un équilibre stratégique, souvent dicté par le temps et l'argent.

Le coût élevé de la précision

Collecter plus d'échantillons coûte du temps et des ressources. De même, les instruments de haute précision, parfaitement calibrés, sont coûteux. Vous devez décider où investir.

Dépenser beaucoup d'argent dans une taille d'échantillon massive est un gaspillage si vos résultats sont finalement limités par un outil de mesure bon marché et imprécis.

Le point de rendement décroissant

Il y a un point où l'augmentation de la taille de l'échantillon n'apporte presque aucun avantage. Si votre outil de mesure a une erreur aléatoire inhérente de ±2 unités, vous ne pourrez jamais atteindre un intervalle de confiance final plus petit que cela, quel que soit le nombre d'échantillons que vous prélevez.

De même, acheter un instrument de plusieurs millions de dollars est inutile si vous ne prévoyez de prendre que trois échantillons, car votre erreur d'échantillonnage massive éclipsera l'incroyable précision de l'instrument.

L'erreur impardonnable : le biais

N'oubliez pas que l'augmentation de la taille de l'échantillon aide à moyenner le bruit aléatoire, mais ne fait absolument rien pour corriger le biais systématique.

Calibrer vos instruments pour éliminer les erreurs systématiques est souvent l'étape la plus importante que vous puissiez prendre pour garantir l'intégrité de vos données, quelle que soit la taille de l'échantillon.

Concevoir votre stratégie de mesure

Il n'y a pas de taille d'échantillon ou de niveau de précision "correct" unique. Le bon choix dépend entièrement de votre objectif et de vos contraintes.

• Si votre objectif principal est une étude exploratoire rapide : Une taille d'échantillon plus petite combinée à un instrument modérément précis peut être suffisante pour identifier les tendances majeures et orienter les recherches futures.
• Si votre objectif principal est une validation à haute confiance (par exemple, approbation réglementaire) : Vous avez besoin à la fois d'un échantillon large et soigneusement sélectionné et d'un instrument très précis et calibré pour minimiser à la fois l'erreur d'échantillonnage et l'erreur de mesure à un degré vérifiable.
• Si votre instrument de mesure est connu pour être imprécis : Vous pouvez compenser en augmentant considérablement la taille de votre échantillon, mais seulement si l'erreur est aléatoire, et non systématique. Cela réduira votre incertitude globale, mais seulement jusqu'à la limite fixée par les défauts de l'instrument.
• Si la collecte d'échantillons est extrêmement coûteuse ou difficile (par exemple, exploration spatiale) : Vous devez investir dans l'instrument de mesure le plus précis possible pour extraire la valeur maximale de chaque point de donnée précieux.

En fin de compte, équilibrer la taille de l'échantillon et la précision des mesures consiste à allouer stratégiquement vos ressources pour combattre les sources d'incertitude les plus importantes dans votre contexte spécifique.

Tableau récapitulatif :

Facteur	Effet sur les résultats	Comment améliorer
Grande taille d'échantillon	Réduit l'erreur d'échantillonnage ; rend l'erreur de mesure plus significative.	Augmenter le nombre d'échantillons mesurés.
Haute précision de mesure	Réduit l'erreur d'instrument ; crucial lorsque l'erreur d'échantillonnage est faible.	Utiliser un équipement précis et bien calibré.
Erreur systématique (biais)	Ne peut pas être réduite en augmentant la taille de l'échantillon.	Calibrer régulièrement les instruments.
Erreur aléatoire (bruit)	Peut être réduite en faisant la moyenne de plus de mesures.	Utiliser un équipement fiable et répéter les mesures.

Prêt à obtenir des résultats précis et fiables dans votre laboratoire ?

Le juste équilibre entre la taille de l'échantillon et la précision des mesures est essentiel pour l'intégrité de vos données. KINTEK est spécialisé dans les équipements de laboratoire de haute précision et les consommables, répondant à tous vos besoins en laboratoire. Que vous ayez besoin d'instruments d'une précision supérieure pour de petits ensembles d'échantillons ou d d'équipements robustes pour des études à grande échelle, nous avons la solution pour minimiser votre erreur totale et maximiser la confiance dans vos résultats.

Contactez-nous dès aujourd'hui pour discuter de la manière dont nos produits peuvent améliorer votre stratégie de mesure. Laissez nos experts vous aider à sélectionner les outils parfaits pour votre application spécifique.

#FormulaireDeContact