Quels sont les facteurs qui affectent la taille de l'échantillon ? Optimisez la puissance et la précision de votre étude

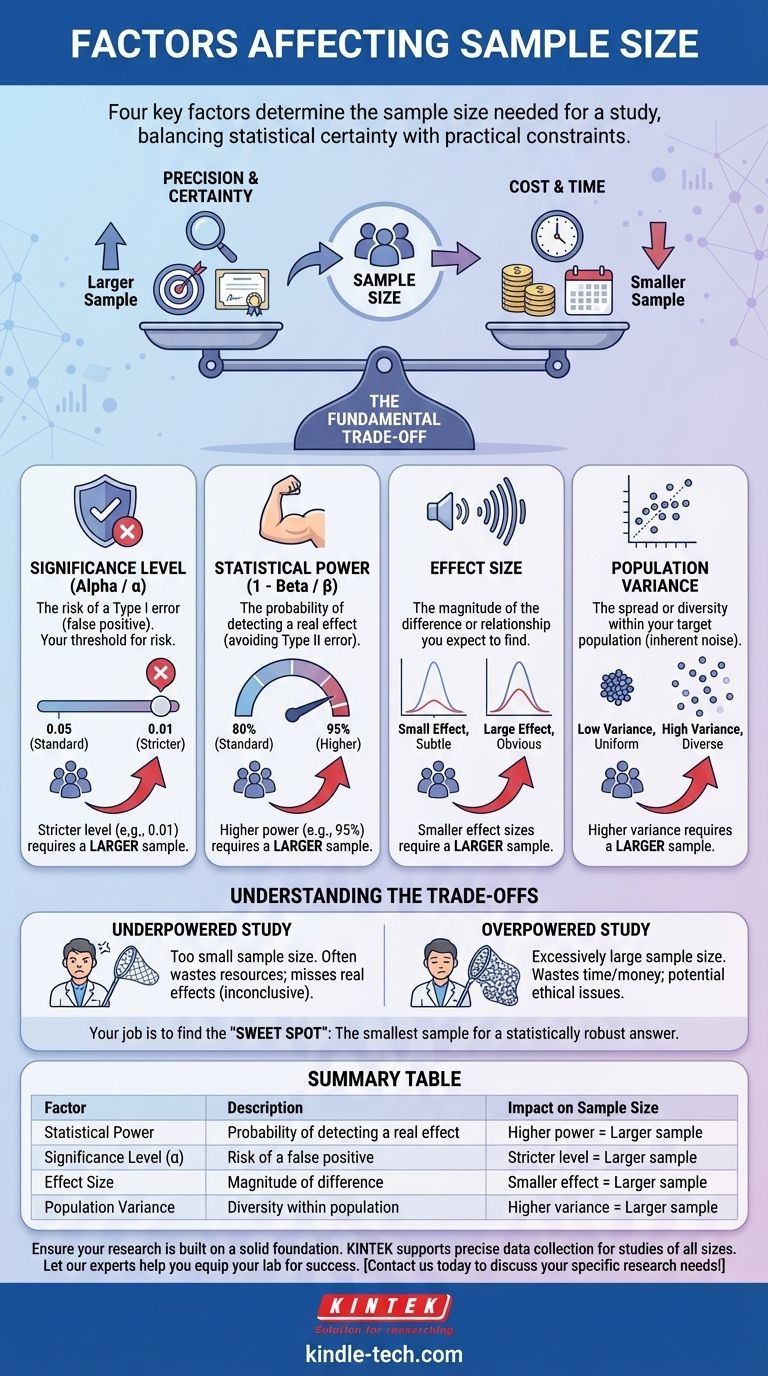
En fin de compte, quatre facteurs clés déterminent la taille de l'échantillon dont vous avez besoin pour une étude : la puissance statistique souhaitée, le niveau de signification que vous définissez, la taille de l'effet que vous souhaitez détecter et la variabilité au sein de la population que vous étudiez. Ces éléments travaillent ensemble pour équilibrer le besoin de certitude statistique avec des contraintes pratiques comme le temps et le budget.

Le principal défi du choix de la taille de l'échantillon est de gérer un compromis fondamental. Vous équilibrez le désir de précision et de certitude (qui nécessite un échantillon plus grand) avec les limitations pratiques de coût et de temps (qui poussent à un échantillon plus petit).

Les concepts statistiques fondamentaux qui déterminent la taille de l'échantillon

Pour prendre une décision éclairée, vous devez d'abord comprendre les principes statistiques en jeu. Ce ne sont pas seulement des règles abstraites ; ce sont les leviers que vous pouvez actionner pour contrôler la fiabilité de vos résultats.

Niveau de signification (Alpha / α)

Le niveau de signification, souvent fixé à 0,05 (ou 5 %), est votre seuil de risque. Il représente la probabilité de commettre une "erreur de type I" – conclure qu'il y a un effet alors qu'en réalité, il n'y en a pas.

Un alpha plus petit (par exemple, 0,01) signifie que vous êtes plus prudent et que vous voulez être plus certain avant d'affirmer qu'un résultat est significatif. Cette norme plus stricte nécessite une taille d'échantillon plus grande pour satisfaire la charge de la preuve plus élevée.

Puissance statistique (1 - Bêta / β)

La puissance est la probabilité que votre étude détecte un effet s'il y en a réellement un. C'est l'inverse d'une "erreur de type II" (ne pas trouver un effet réel).

Une norme courante pour la puissance est de 80 %. Augmenter votre puissance souhaitée à 90 % ou 95 % réduit votre risque de manquer une découverte authentique, mais cette certitude accrue nécessite une taille d'échantillon plus grande.

Taille de l'effet

La taille de l'effet est l'ampleur de la différence ou de la relation que vous vous attendez à trouver. C'est le signal que vous essayez de détecter.

Détecter un effet petit et subtil, c'est comme essayer d'entendre un murmure dans une pièce bondée ; vous devez écouter très attentivement (c'est-à-dire utiliser un grand échantillon). Détecter un effet grand et évident, c'est comme entendre un cri ; c'est facile à remarquer même avec un petit échantillon. Par conséquent, les effets de petite taille nécessitent des échantillons plus grands.

Variance de la population

La variance (ou l'écart-type) mesure la dispersion ou la diversité au sein de votre population cible. Elle représente le "bruit" inhérent à vos données.

Si une population présente une très faible variabilité (par exemple, la plupart des gens sont très similaires), un petit échantillon est suffisant pour la représenter. Si la population est très diverse avec beaucoup de variabilité, vous avez besoin d'un échantillon plus grand pour capturer cette diversité et distinguer le signal du bruit.

Comprendre les compromis

Le choix de la taille de l'échantillon n'est jamais un exercice purement mathématique. Il implique des décisions stratégiques concernant les ressources et les niveaux de risque acceptables.

Le risque d'une étude sous-puissante

Une étude dont la taille de l'échantillon est trop petite est considérée comme "sous-puissante". C'est le piège le plus courant.

Une étude sous-puissante est souvent un gaspillage complet de ressources. Même si un effet réel existe, l'étude manque de puissance statistique pour le détecter, ce qui conduit à un résultat "négatif" non concluant ou trompeur.

L'inefficacité d'une étude sur-puissante

Inversement, une taille d'échantillon excessivement grande est "sur-puissante". Bien qu'elle offre une grande précision, elle gaspille du temps et de l'argent.

Dans la recherche clinique ou utilisateur, cela peut également être contraire à l'éthique, car cela expose plus de participants que nécessaire à des risques ou des interventions potentiels pour un résultat qui aurait pu être confirmé avec moins de points de données.

Précision vs. Praticité

Le conflit central est clair. Les statisticiens préconiseront toujours des échantillons plus grands pour augmenter la certitude. Les chefs de projet et les responsables budgétaires pousseront pour des échantillons plus petits afin d'économiser des ressources.

Votre travail consiste à trouver le "juste milieu" : la plus petite taille d'échantillon qui fournit une réponse statistiquement robuste et crédible à votre question de recherche.

Comment déterminer la taille de votre échantillon

Pour avancer, vous devez définir vos priorités. La bonne taille d'échantillon dépend entièrement de l'objectif de votre étude et des ressources dont vous disposez.

• Si votre objectif principal est de détecter un effet très petit et subtil : Vous devez vous engager à utiliser une grande taille d'échantillon, car c'est la seule façon d'avoir une puissance suffisante.
• Si votre objectif principal est une étude exploratoire avec un budget limité : Vous devrez peut-être accepter une puissance plus faible ou ne viser que la détection d'effets plus grands et plus évidents.
• Si votre objectif principal est de minimiser le risque de faux négatifs (manquer un effet réel) : Vous devez augmenter la puissance statistique (par exemple, à 90 %), ce qui nécessitera un échantillon plus grand.
• Si votre objectif principal est de minimiser le risque de faux positifs (affirmer un effet qui n'est pas réel) : Vous devez utiliser un niveau de signification plus strict (par exemple, 0,01), ce qui augmente également la taille d'échantillon requise.

Une taille d'échantillon judicieusement choisie est le fondement d'une recherche crédible et fiable.

Tableau récapitulatif :

Facteur	Description	Impact sur la taille de l'échantillon
Puissance statistique	Probabilité de détecter un effet réel	Puissance plus élevée = Échantillon plus grand
Niveau de signification (α)	Risque de faux positif (erreur de type I)	Niveau plus strict (ex. 0,01) = Échantillon plus grand
Taille de l'effet	Amplitude de la différence ou de la relation	Effet plus petit = Échantillon plus grand
Variance de la population	Diversité ou dispersion au sein de la population	Variance plus élevée = Échantillon plus grand

Assurez-vous que votre recherche repose sur des bases solides. Choisir la bonne taille d'échantillon est essentiel pour obtenir des résultats crédibles et fiables. KINTEK est spécialisé dans la fourniture d'équipements de laboratoire et de consommables qui soutiennent une collecte de données précise pour des études de toutes tailles. Laissez nos experts vous aider à équiper votre laboratoire pour le succès. Contactez-nous dès aujourd'hui pour discuter de vos besoins de recherche spécifiques !