Comment une plus grande surface affecte-t-elle la pression d'une même force ? Maîtrisez la physique de la répartition des forces

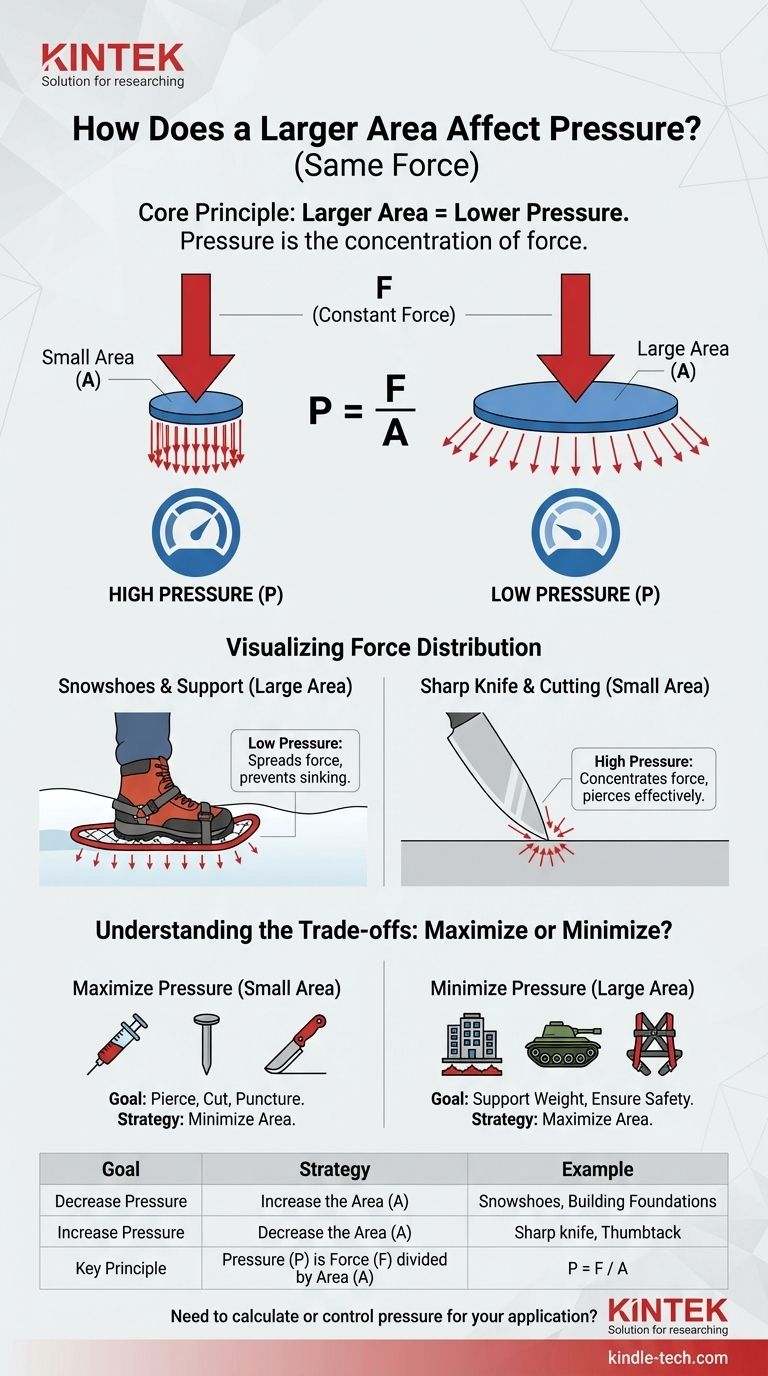
En bref, une plus grande surface diminue la pression exercée par une même force. La relation est inversement proportionnelle : à mesure que la surface sur laquelle une force constante est appliquée augmente, la pression en tout point donné de cette surface diminue. Cela s'explique par le fait que la même quantité de force est répartie sur une surface plus large.

Le principe fondamental à comprendre est que la pression n'est pas la force elle-même, mais la concentration de la force. En augmentant la surface de contact, vous diluez efficacement la force, ce qui entraîne une réduction de la pression.

La relation fondamentale : Pression, Force et Surface

Pour vraiment saisir ce concept, nous devons examiner la physique simple mais puissante qui le sous-tend. L'interaction entre ces trois éléments régit tout, de la façon dont un couteau coupe à la façon dont un bâtiment tient debout.

L'équation fondamentale

La relation est définie par l'équation P = F / A.

• P signifie Pression, qui est la quantité de force exercée par unité de surface.
• F signifie Force, qui est la poussée ou la traction exercée sur un objet (comme le poids).
• A signifie Surface, qui est la surface sur laquelle la force est distribuée.

Cette formule montre clairement que si la Force (F) reste constante, l'augmentation de la Surface (A) au dénominateur entraînera inévitablement une diminution de la Pression (P) résultante.

Une analogie intuitive : Un lit de clous

Imaginez que vous essayez de vous tenir debout sur un seul clou. Tout votre poids corporel (la force) serait concentré sur la petite pointe de ce clou, créant une pression immense qui percerait facilement votre pied.

Maintenant, imaginez un lit de milliers de clous. Lorsque vous vous allongez, votre même poids corporel est maintenant réparti uniformément sur les pointes de tous ces clous. La surface totale est énorme, de sorte que la pression de chaque clou est incroyablement faible et insuffisante pour percer votre peau. La force n'a pas changé, mais la surface a changé, modifiant radicalement le résultat.

Visualisation de la répartition des forces

Considérez la force comme une quantité fixe d'eau et la surface comme le récipient dans lequel vous la versez.

Si vous versez l'eau dans un verre haut et fin (une petite surface), le niveau d'eau sera élevé (haute pression). Si vous versez la même quantité d'eau dans une casserole large et peu profonde (une grande surface), le niveau d'eau sera très bas (basse pression). La quantité d'eau n'a jamais changé, seule sa concentration.

Exemples pratiques dans la vie quotidienne

Ce principe n'est pas seulement théorique ; c'est un aspect fondamental de l'ingénierie et de la conception avec lequel vous interagissez constamment.

Pourquoi les raquettes à neige fonctionnent

Le poids d'une personne (force) est constant. Lorsque vous portez une botte normale, cette force est concentrée sur la petite surface de la semelle, ce qui vous fait vous enfoncer dans la neige. Les raquettes à neige augmentent considérablement la surface, répartissant votre poids et abaissant la pression bien en dessous de ce que la neige peut supporter.

Le tranchant d'un couteau

Un couteau aiguisé a une surface de contact extrêmement petite sur son tranchant. Cette conception concentre la force que vous appliquez, créant une pression immense qui peut facilement trancher les matériaux. Un couteau émoussé a une surface plus grande et émoussée, ce qui répartit la force et nécessite beaucoup plus d'effort pour obtenir la même pression de coupe.

Fondations des bâtiments

Les gratte-ciel sont incroyablement lourds. Pour éviter qu'ils ne s'enfoncent dans le sol, ils sont construits sur des fondations en béton larges et massives. Ces fondations répartissent l'immense poids (force) du bâtiment sur une très grande surface, garantissant que la pression exercée sur le sol est suffisamment faible pour être supportée en toute sécurité.

Punaises et aiguilles

Une punaise est un exemple parfait de manipulation de ce principe. Elle a une tête large et plate pour votre pouce (grande surface, basse pression pour le confort) et une pointe acérée et minuscule pour le mur (petite surface, haute pression pour une perforation facile).

Comprendre les compromis

L'objectif n'est pas toujours de diminuer la pression. La conception optimale dépend entièrement de la fonction prévue, et les ingénieurs doivent choisir de concentrer ou de distribuer la force.

Quand une pression élevée est l'objectif

Dans de nombreuses applications, l'objectif est de maximiser la pression. Ceci est réalisé en minimisant la surface de contact pour concentrer la force appliquée.

Les exemples incluent les aiguilles d'injection, les clous, les outils de coupe et les patins à glace. Le but de ces conceptions est de créer une pression suffisamment élevée pour percer une surface avec un minimum de force.

Quand une basse pression est critique

Inversement, minimiser la pression est souvent une question de sécurité, de stabilité ou de préservation. Ceci est réalisé en maximisant la surface de contact.

Les exemples incluent les larges chenilles d'un char ou d'un bulldozer, les larges bretelles d'un sac à dos lourd et les harnais de sécurité qui répartissent la force d'une chute sur le torse.

Faire le bon choix pour votre objectif

Comprendre comment manipuler la relation entre la force, la pression et la surface est essentiel pour résoudre d'innombrables défis physiques.

• Si votre objectif principal est de percer, couper ou perforer : Vous devez concentrer votre force en rendant la surface de contact aussi petite que possible.
• Si votre objectif principal est de supporter un poids ou d'éviter de s'enfoncer : Vous devez distribuer votre force en rendant la surface de contact aussi grande que possible.
• Si votre objectif principal est d'assurer la sécurité lors d'un impact : Vous devez dissiper la force sur la plus grande surface possible pour minimiser la pression sur un point unique.

Maîtriser ce seul principe vous permet de concevoir et de construire des outils plus efficaces et des structures plus sûres.

Tableau récapitulatif :

Objectif	Stratégie	Exemple
Diminuer la Pression	Augmenter la Surface (A)	Raquettes à neige, fondations de bâtiments
Augmenter la Pression	Diminuer la Surface (A)	Couteau aiguisé, punaise, lame de patin à glace
Principe Clé	La Pression (P) est la Force (F) divisée par la Surface (A)	P = F / A

Besoin de calculer ou de contrôler la pression pour votre application ? KINTEK est spécialisé dans les équipements et consommables de laboratoire, fournissant les outils et l'expertise pour vous aider à appliquer ces principes fondamentaux dans vos processus de recherche ou de contrôle qualité. Que vous conceviez un nouveau produit ou optimisiez une procédure, notre équipe peut vous aider à sélectionner l'équipement approprié pour mesurer et gérer la force et la pression avec précision.

Contactez nos experts dès aujourd'hui pour discuter de vos besoins spécifiques !

Guide Visuel