En bref, il n'existe pas de terme standard appelé "diamètre de chiralité". Au lieu de cela, le diamètre d'un nanotube de carbone (CNT) est une conséquence physique directe de sa chiralité, qui décrit l'angle et la géométrie spécifiques de sa structure atomique. La chiralité est définie par une paire d'entiers, (n,m), qui dictent précisément comment une feuille de graphène est conceptuellement "enroulée" pour former le tube.
Le concept central est que le diamètre d'un nanotube de carbone n'est pas une valeur arbitraire, mais une propriété discrète mathématiquement liée à sa structure atomique. Comprendre les indices chiraux (n,m) permet de calculer son diamètre exact, ce qui prédit à son tour ses propriétés électroniques et physiques fondamentales.
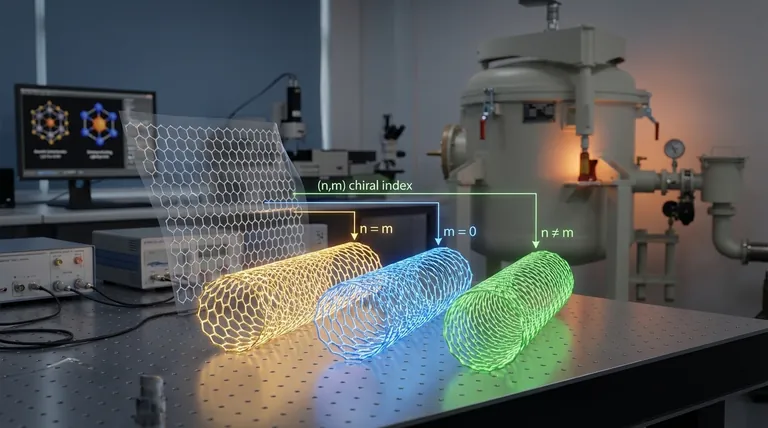
De la feuille de graphène au nanotube
Le concept de chiralité
Imaginez une feuille plate de graphène, une seule couche d'atomes de carbone disposés en réseau en nid d'abeille. Un nanotube de carbone est formé en enroulant cette feuille en un cylindre sans soudure.
La chiralité est le terme utilisé pour décrire l'angle et la direction précis dans lesquels vous enroulez la feuille. Ce n'est pas un processus arbitraire ; il est défini par un vecteur chiral, noté Ch.
Les indices chiraux (n,m)
Le vecteur chiral est défini par deux entiers, (n,m), qui représentent le nombre de pas que vous effectuez le long des deux directions principales du réseau de graphène pour passer d'un point à un point identique après l'enroulement.
Ces indices définissent de manière unique la structure entière du nanotube. En fonction de leurs valeurs, les CNT sont classés en trois types principaux :
- Fauteuil (Armchair) : Lorsque n = m, par exemple (10,10).
- Zigzag : Lorsque m = 0, par exemple (17,0).
- Chiral : Toutes les autres combinaisons où n ≠ m et m ≠ 0, par exemple (12,8).
Calcul du diamètre à partir de la chiralité
La formule du diamètre
Une fois que vous connaissez les indices (n,m) d'un nanotube, son diamètre (d) peut être calculé avec une formule mathématique précise.
La formule est :
d = (a / π) * √(n² + m² + nm)
Cette équation relie directement les indices abstraits (n,m) à une dimension physique mesurable.
Comprendre les variables
Dans la formule, 'a' est la constante de réseau du graphène. Cette valeur est dérivée de la longueur fondamentale de la liaison carbone-carbone (a_cc), qui est d'environ 0,142 nanomètres (nm).
La constante de réseau a est calculée comme a = a_cc * √3, ce qui la rend approximativement égale à 0,246 nm. La lettre grecque π (pi) est la constante mathématique, environ 3,14159.
Pourquoi le diamètre est un paramètre critique
Il dicte les propriétés électroniques
La géométrie exacte déterminée par (n,m) et le diamètre résultant ont un effet profond sur la façon dont les électrons peuvent voyager à travers le nanotube. Cela détermine directement si le CNT se comporte comme un métal ou un semi-conducteur.
Une règle simple est la suivante :
- Les nanotubes fauteuil (n,n) sont toujours métalliques.
- Pour tous les autres types, le nanotube est métallique si (n-m) est un multiple de 3.
- Si (n-m) n'est pas un multiple de 3, le nanotube est semi-conducteur.
Cette propriété explique pourquoi les CNT sont si prometteurs pour l'électronique de nouvelle génération ; vous pouvez avoir un fil métallique ou un composant de transistor semi-conducteur à partir du même élément, simplement en changeant sa géométrie.
Il influence les propriétés physiques et optiques
Le diamètre affecte également la résistance mécanique, la rigidité et les longueurs d'onde spécifiques de la lumière qu'un nanotube absorbera ou émettra.
Les tubes de plus petit diamètre sont généralement plus rigides, tandis que la bande interdite électronique des CNT semi-conducteurs est inversement proportionnelle à leur diamètre.
Le défi pratique : le contrôle de la synthèse
Le problème de la chiralité mixte
Le principal défi pour exploiter la puissance des CNT est de contrôler leur synthèse. La plupart des méthodes de production, comme le dépôt chimique en phase vapeur (CVD), produisent un mélange de nanotubes avec de nombreuses valeurs (n,m) différentes.
Il en résulte un échantillon contenant un mélange de diamètres différents, y compris des tubes métalliques et semi-conducteurs.
L'obstacle pour les applications
Ce manque d'uniformité est un obstacle majeur. Pour une puce informatique, vous avez besoin de nanotubes purement semi-conducteurs. Pour un film conducteur transparent, vous pourriez vouloir des nanotubes purement métalliques.
La séparation de ce mélange — un processus appelé "tri" — est un domaine complexe et coûteux de recherche continue. L'incapacité à produire à faible coût des CNT à chiralité unique à grande échelle est ce qui limite actuellement leur application commerciale généralisée en électronique.
Faire le bon choix pour votre objectif
- Si votre objectif principal est de créer un fil électronique à l'échelle nanométrique : Vous avez besoin d'un CNT métallique. Le choix le plus fiable est un tube fauteuil (n,n), car sa nature métallique est garantie.
- Si votre objectif principal est de construire un transistor à effet de champ (FET) : Vous avez besoin d'un CNT semi-conducteur. Vous devez sélectionner une combinaison (n,m) où (n-m) n'est pas un multiple de 3.
- Si votre objectif principal est le renforcement mécanique dans un matériau composite : Un mélange de chiralités peut être acceptable, mais le contrôle de la distribution des diamètres peut aider à optimiser la résistance et le transfert de charge.
- Si votre objectif principal est les applications optiques comme les capteurs : Vous avez besoin d'un CNT semi-conducteur spécifique dont le diamètre fournit la bande interdite exacte requise pour interagir avec une longueur d'onde de lumière cible.
En fin de compte, la puissance des indices (n,m) est qu'ils fournissent un plan direct de la structure atomique aux propriétés fonctionnelles.
Tableau récapitulatif :
| Type de CNT | Chiralité (n,m) | Propriété clé |
|---|---|---|
| Fauteuil (Armchair) | n = m (par exemple, 10,10) | Toujours métallique |
| Zigzag | m = 0 (par exemple, 17,0) | Métallique si (n-m) est un multiple de 3 |
| Chiral | n ≠ m, m ≠ 0 (par exemple, 12,8) | Semi-conducteur si (n-m) n'est pas un multiple de 3 |
Prêt à faire progresser votre recherche sur les nanotubes de carbone ? KINTEK fournit des équipements de laboratoire de précision et des consommables adaptés au développement de la nanotechnologie. Que vous synthétisiez, caractérisiez ou appliquiez des CNT, nos solutions vous aident à atteindre le contrôle de la chiralité et les performances matérielles dont vous avez besoin. Contactez nos experts dès aujourd'hui pour discuter de la manière dont nous pouvons soutenir les défis spécifiques de votre laboratoire en nanomatériaux et au-delà.
Guide Visuel
Produits associés
- Four de graphitation sous vide à ultra-haute température au graphite
- Four de graphitation continue sous vide de graphite
- Grand four de graphitisation sous vide vertical en graphite
- Électrode à disque rotatif (disque-anneau) RRDE / Compatible avec PINE, ALS japonais, Metrohm suisse carbone vitreux platine
- Presse hydraulique de laboratoire, machine de pressage de pastilles pour boîte à gants
Les gens demandent aussi
- Comment le graphite synthétique est-il fabriqué ? Une plongée profonde dans le processus à haute température
- Quelle est la conductivité du graphite ? Comprendre ses propriétés électriques et thermiques élevées
- Quelles sont les propriétés mécaniques du graphite ? Exploiter la rigidité et gérer la fragilité
- Pourquoi le graphite est-il si difficile à faire fondre ? Le secret réside dans sa structure atomique
- À quelle température le graphite fond-il ? Comprendre son changement de phase extrême
